7.3 Sampling Distribution of a Sample Mean Read 451ã¢â‚¬â€œ453

March 07, 2022 Post a Comment

Even if you are non in the field of statistics, you must have come beyond the term "Normal Distribution".

A probability distribution is a statistical function that describes the likelihood of obtaining the possible values that a random variable can take. By this, we mean the range of values that a parameter can take when we randomly pick up values from it.

A probability distribution tin can be discrete or continuous.

Suppose in a city we take heights of adults between the age group of 20-30 years ranging from 4.5 ft. to 7 ft.

If we were asked to choice upwards ane developed randomly and asked what his/her (assuming gender does non bear upon height) height would be? There's no style to know what the height will be. But if we have the distribution of heights of adults in the metropolis, we can bet on the most probable result.

What is Normal Distribution?

A Normal Distribution is likewise known every bit a Gaussian distribution or famously Bell Curve. People employ both words interchangeably, but it means the same thing. It is a continuous probability distribution.

The probability density function (pdf) for Normal Distribution:

Probability Density Function Of Normal Distribution — **Probability Density Office Of Normal Distribution**

where, μ = Mean , σ = Standard deviation , x = input value.

Terminology:

Mean – The mean is the usual average. The sum of full points divided by the full number of points.
Standard Divergence – Standard departure tells the states how "spread out" the data is. It is a mensurate of how far each observed value is from the mean.

Looks daunting, isn't it? Simply information technology is very simple.

1. Example Implementation of Normal Distribution

Permit's have a expect at the code below. We'll utilise numpy and matplotlib for this demonstration:

# Importing required libraries  import numpy as np import matplotlib.pyplot equally plt  # Creating a series of data of in range of 1-50. x = np.linspace(ane,fifty,200)  #Creating a Office. def normal_dist(x , mean , sd):     prob_density = (np.pi*sd) * np.exp(-0.5*((10-mean)/sd)**2)     return prob_density  #Calculate mean and Standard deviation. mean = np.mean(x) sd = np.std(x)  #Utilise function to the data. pdf = normal_dist(x,mean,sd)  #Plotting the Results plt.plot(x,pdf , color = 'reddish') plt.xlabel('Data points') plt.ylabel('Probability Density')

2. Properties of Normal Distribution

The normal distribution density role simply accepts a data indicate along with a mean value and a standard deviation and throws a value which nosotros call probability density.

Nosotros can alter the shape of the bell curve by changing the hateful and standard departure.

Changing the mean will shift the curve towards that mean value, this ways we can change the position of the curve by altering the hateful value while the shape of the curve remains intact.

The shape of the curve tin be controlled by the value of Standard divergence. A smaller standard divergence will result in a closely divisional bend while a high value will result in a more spread out curve.

Some first-class properties of a normal distribution:

The hateful, mode, and median are all equal.
The full area under the curve is equal to 1.
The bend is symmetric around the mean.

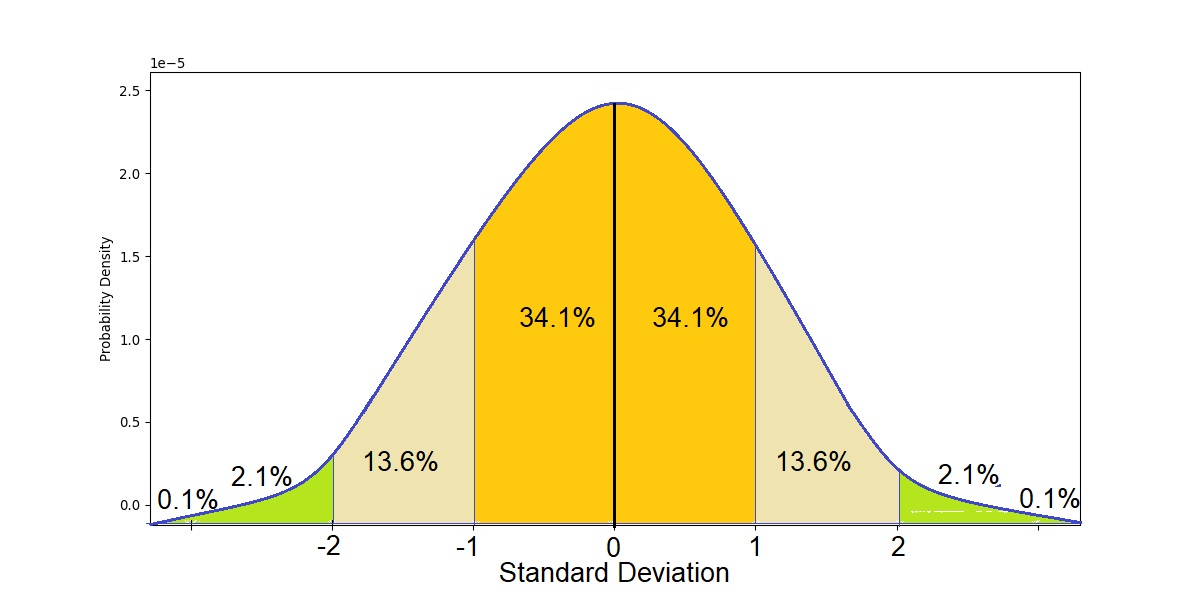
Percentage Distribution of Data Around Mean — Percentage Distribution of Data Effectually Hateful

Empirical rule tells usa that:

68% of the data falls within ane standard departure of the mean.
95% of the data falls within two standard deviations of the mean.
99.7% of the data falls within three standard deviations of the mean.

It is by far i of the most important distributions in all of the Statistics. The normal distribution is magical because most of the naturally occurring miracle follows a normal distribution. For example, blood pressure level, IQ scores, heights follow the normal distribution.

Calculating Probabilities with Normal Distribution

To notice the probability of a value occurring within a range in a normal distribution, nosotros just need to find the area under the curve in that range. i.east. nosotros need to integrate the density function.

Since the normal distribution is a continuous distribution, the area under the curve represents the probabilities.

Before getting into details showtime let'southward just know what a Standard Normal Distribution is.

A standard normal distribution is just similar to a normal distribution with hateful = 0 and standard deviation = i.

Z = (x-μ)/ σ

The z value above is also known as a z-score. A z-score gives y'all an idea of how far from the mean a information point is.

If nosotros intend to calculate the probabilities manually nosotros volition need to lookup our z-value in a z-tabular array to see the cumulative percentage value. Python provides us with modules to do this work for us. Permit's go into it.

1. Creating the Normal Curve

We'll use scipy.norm class part to calculate probabilities from the normal distribution.

Suppose we take data of the heights of adults in a boondocks and the data follows a normal distribution, we have a sufficient sample size with mean equals five.3 and the standard deviation is 1.

This information is sufficient to brand a normal curve.

# import required libraries from scipy.stats import norm import numpy as np import matplotlib.pyplot as plt import seaborn as sb  # Creating the distribution data = np.arange(i,10,0.01) pdf = norm.pdf(data , loc = 5.three , scale = one )  #Visualizing the distribution  sb.set_style('whitegrid') sb.lineplot(data, pdf , color = 'black') plt.xlabel('Heights') plt.ylabel('Probability Density')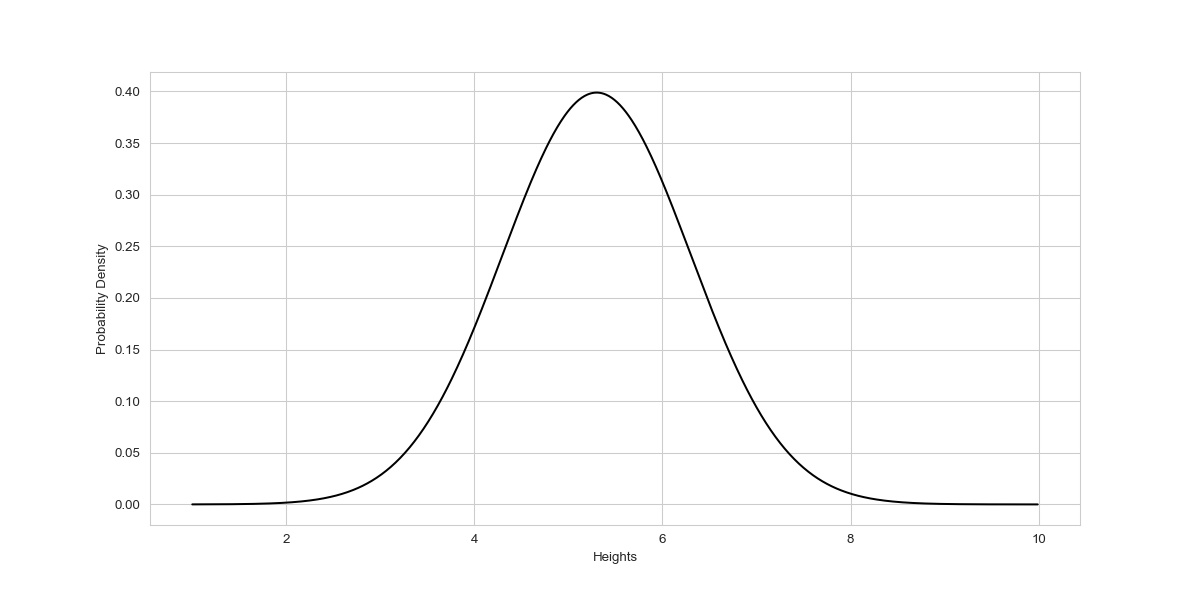

The norm.pdf( ) class method requires loc and scale along with the data as an input argument and gives the probability density value. loc is nothing but the hateful and the scale is the standard departure of data. the code is similar to what we created in the prior section only much shorter.

2. Calculating Probability of Specific Information Occurance

At present, if we were asked to pick one person randomly from this distribution, then what is the probability that the height of the person volition exist smaller than iv.v ft. ?

Area Under The Curve As Probability — Surface area Under The Bend As Probability

The area under the bend as shown in the figure above volition be the probability that the height of the person will exist smaller than 4.5 ft if called randomly from the distribution. Allow'southward see how nosotros can calculate this in python.

The area under the curve is nothing just only the Integration of the density function with limits equals -∞ to 4.5.

norm(loc = 5.3 , scale = one).cdf(4.v)

                0.211855 or 21.185 %

The unmarried line of lawmaking above finds the probability that at that place is a 21.18% chance that if a person is chosen randomly from the normal distribution with a mean of 5.3 and a standard deviation of 1, then the tiptop of the person volition be below 4.5 ft.

We initialize the object of class norm with mean and standard deviation, then using .cdf( ) method passing a value up to which nosotros need to find the cumulative probability value. The cumulative distribution function (CDF) calculates the cumulative probability for a given 10-value.

Cumulative probability value from -∞ to ∞ will be equal to ane.

Now, again we were asked to pick one person randomly from this distribution, and so what is the probability that the meridian of the person volition be betwixt 6.5 and iv.5 ft. ?

Area Under The Curve as a probability calculation — Area Nether The Curve Between four.5 And 6.5 Ft

cdf_upper_limit = norm(loc = 5.3 , calibration = ane).cdf(6.v) cdf_lower_limit = norm(loc = 5.iii , scale = i).cdf(4.v)  prob = cdf_upper_limit - cdf_lower_limit print(prob)

                0.673074 or 67.30 %

The above code first calculated the cumulative probability value from -∞ to vi.5 and then the cumulative probability value from -∞ to 4.five. if we subtract cdf of iv.5 from cdf of 6.5 the event we get is the area nether the curve between the limits 6.5 and four.5.

Now, what if we were asked almost the probability that the height of a person chosen randomly will be above half-dozen.5ft?

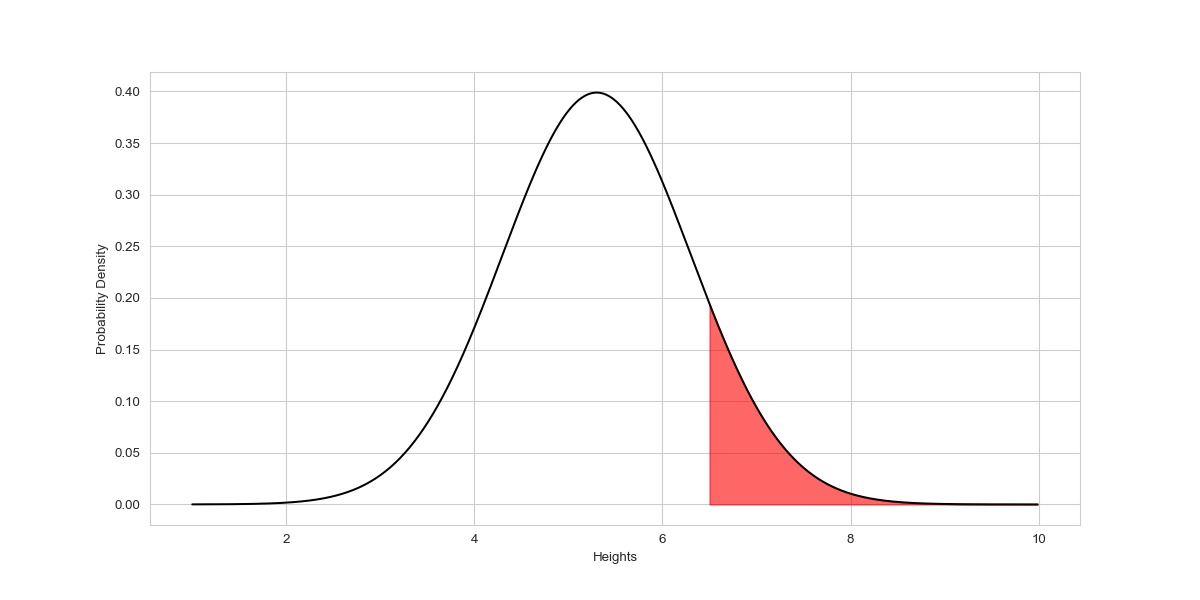
Area Under The Curve Between a value And Infinity — Area Nether The Curve Between 6.5ft and Infinity

It's elementary, as we know the full area under the curve equals one, and if nosotros calculate the cumulative probability value from -∞ to 6.5 and subtract it from ane, the result will be the probability that the pinnacle of a person called randomly will be above vi.5ft.

cdf_value = norm(loc = 5.iii , scale = 1).cdf(half-dozen.5) prob = 1- cdf_value impress(prob)

                0.115069 or xi.l %.

That'due south a lot to sink in, but I encourage all to go on practicing this essential concept along with the implementation using python.

The consummate code from above implementation:

# import required libraries from scipy.stats import norm import numpy equally np import matplotlib.pyplot equally plt import seaborn as sb  # Creating the distribution data = np.arange(1,10,0.01) pdf = norm.pdf(data , loc = v.3 , scale = ane )  #Probability of height to be under 4.five ft. prob_1 = norm(loc = five.3 , scale = 1).cdf(4.5) print(prob_1)  #probability that the elevation of the person will exist between 6.5 and 4.5 ft.  cdf_upper_limit = norm(loc = 5.3 , scale = i).cdf(six.5) cdf_lower_limit = norm(loc = 5.3 , calibration = i).cdf(iv.5)  prob_2 = cdf_upper_limit - cdf_lower_limit print(prob_2)  #probability that the height of a person called randomly will be above six.5ft  cdf_value = norm(loc = 5.three , scale = one).cdf(six.5) prob_3 = 1- cdf_value print(prob_3)